
Sine, cosine and tangent are trigonometric functions of an angle. The sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent side to that of the hypotenuse. The tangent is the ratio of the opposite side to the adjacent side.



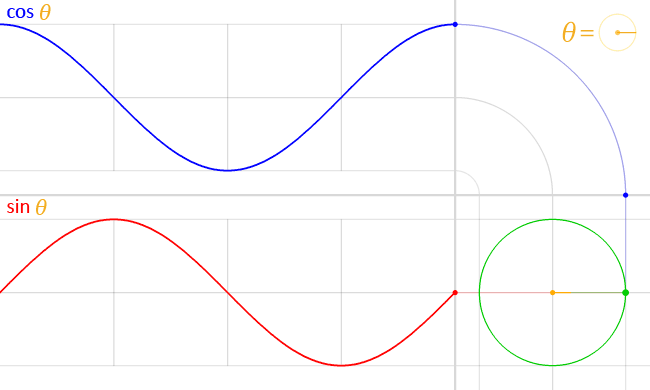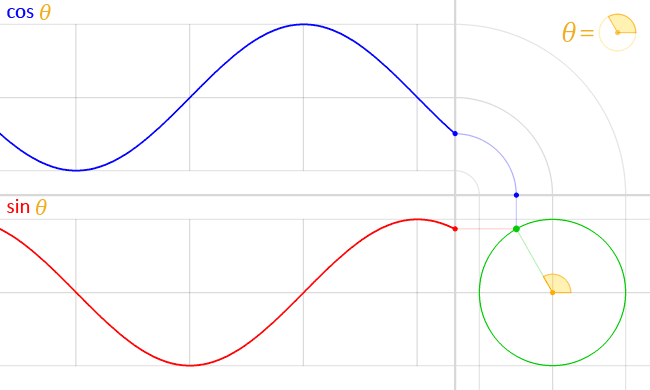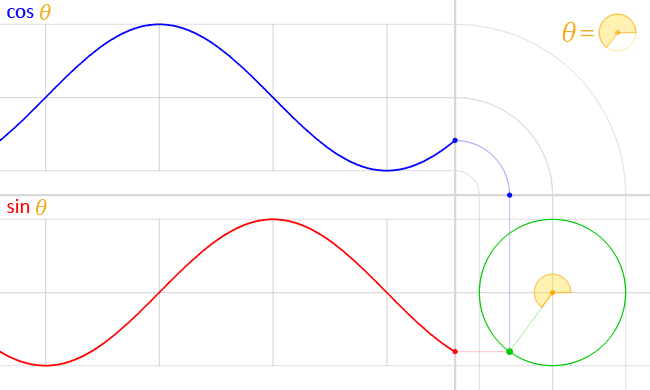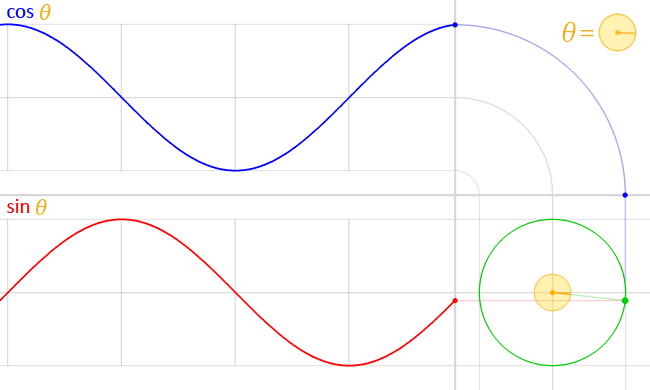
The sine can be interpreted as the height above the diameter on circumference at angle $\theta$ in a unit circle (In trigonometry, a unit circle is the circle of radius one centered at the origin (0, 0) ).



The trigonometric functions cosine and sine of angle θ may be defined on the unit circle as follows: if (x, y) is a point on the unit circle, and if the ray from the origin (0, 0) to (x, y) makes an angle θ from the positive x-axis, (where counterclockwise turning is positive), then
$$ \cos\theta = x \; \; and \; \; \sin\theta = y $$
Then, the equation $x^2 + y^2 = 1$ gives the relation
$\cos^2\theta + \sin^2\theta = 1$
The unit circle also demonstrates that sine and cosine are periodic functions (they repeat their values after each full rotation (360 degrees or 2π radians) around the unit circle) , with the identities
$\cos \theta = \cos(2 \pi k + \theta)$
$\sin \theta = \sin(2 \pi k + \theta)$
for any integer $k$.
Unfolding the circumference of the circle on an the $x$ axis and computing the sine and cosine for each point gives us the sine and cosine waves.

The formula for a generic sine wave is:
$$ x(t) = A\sin(2\pi ft + \theta) $$
where $A$ is the amplitude, $f$ the frequency and $\theta$ the phase.

When a sine wave has $\theta = 0$ we call it a sine, when it has $\theta = \frac{\pi}{2}$ a cosine. Sine and cosine are orthogonal to each other.